RTT 측정 방법
RTT란 Round Trip Time의 약자다. 한마디로 기차가 목적지까지 갔다가 오는데 걸리는 시간을 생각하면 된다. 서울-부산간 KTX라면 한 6시간쯤 되겠다. RTT 측정을 위해서 사용된 클라이언트의 사양은 <표 1>에 나타나 있다
표 1 실험에 사용된 클라이언트 사양
Amd Turion 64 (1.7 GHz)
1GB Ram
10MB ADSL 라인
Windows XP SP2
RTT 측정을 손쉽게 하기 위해서 블로킹 I/O 모델을 사용하였다. 블로킹 I/O 모델의 경우 정확하게 어느 시점에 완료되었는지 판단하기가 손쉽기 때문이다. RTT의 정확한 시간 측정을 위해서 QueryPerformanceCounter가 사용되었다. 실제로 RTT 측정에 사용된 코드가 <코드 1>에 나타나 있다.
코드 1 RTT 측정 방법
QueryPerformanceCounter(&g\_SendCounter);
QueryPerformanceCounter(&g\_RecvCounter);
LARGE\_INTEGER tmp;
QueryPerformanceFrequency(&tmp);
\_\_int64 freq = tmp.QuadPart;
\_\_int64 s = g\_SendCounter.QuadPart;
\_\_int64 e = g\_RecvCounter.QuadPart;
\_\_int64 rtt = e – s;
double sec = (double)rtt / freq;s, e는 각각 측정 시작 카운터와 끝 카운터를, freq에는 성능 카운터의 Hz가 저장된다. 최종적으로 sec에는 초 단위의 RTT 시간이 들어가게 된다. 분석의 정확성을 기하기 위해서 출력은 소수점 9자리로 제한했다.
미시적 관점에서의 RTT 측정 결과 분석
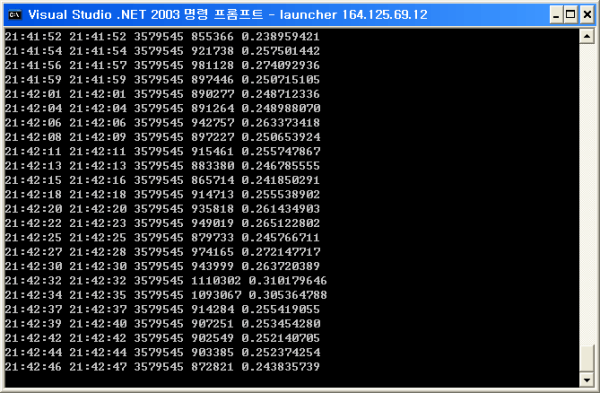
미시적 관점에서의 RTT를 분석하기 위해서 <화면 1>과 같이 오후 9시부터 10시까지 2초 단위로 RTT를 측정하였다. 필드별 의미는 앞에서부터 송신 시간, 수신 시간, 시스템 카운터 주파수, RTT에 소모한 카운터, RTT 시간이다. 측정된 결과의 일부가 <표 2>에 나타나 있다.
<그래프 1>과 <그래프 3>는 측정 결과를 토대로 그린 그래프다. <그래프 1>을 살펴보면 200과 400 사이의 구간에서 한번 RTT 값이 비약적으로 증가한 것을 알 수 있다. 그 외의 구간에서는 대체로 비슷한 수준의 RTT가 측정되었다. <그래프 3>를 그리는데 사용된 자료가 <표 3>에 나타나 있다. 전체 평균은 0.247초 정도로 전체 데이터가 대부분 평균에서 얼마간 벗어 나지 않았다. 살펴 보면 90% 이상의 데이터가 0.2에서 0.3 사이에 집중되어 있는 것을 알 수 있다. (<그래프 2>는 거시적 관점에서의 RTT 분석 그래프와의 비교의 용이성을 위해서 비정상적인 점을 제외하고 그린 그래프다.)
값이 증가한 포인트의 정확한 원인을 알기는 힘들었다. 서버와 클라이언트 모두 특별한 부하가 걸리는 작업은 없었으며, 네트워크 상황 또한 안정적이었다. 단지 한 가지 의심스러운 점은 측정 데이터에서는 제외 되었으나 증가된 지점 직전에 서버로의 접속이 실패한 경우가 있었다는 점이다.
<그래프 1>을 살펴보면 전체적으로 안정된 수준의 RTT 값을 보이다 증가한 다음부터는 다소 변동폭이 커지는 것을 볼 수 있다. 이를 통해서 아마도 클라이언트와 서버 사이의 통신 선로에 부하가 작다가 커졌다가 다시 작아졌다는 것을 유추해 볼 수 있다. 하지만 사실 이 경우의 RTT의 변화폭 또한 0.1초의 범위를 넘어가지 않기 때문에 그다지 큰 변동폭이라 볼 수 없다.
결론적으로 우리는 실험을 통해서 RTT의 경우 안정된 선로에서는 미시적으로 많은 변화를 가지지는 않는다는 것을 알 수 있었다. 학교의 LAN 환경과 ADSL모두 유선을 통해서 연결되어 있으므로 굉장히 안정적인 라인이라고 할 수 있다. RTT 값이 미시적으로 굉장히 변동이 큰 경우에는 네트워크의 장애가 있는 경우라고 할 수 있다. 흔히 하는 테스트로 ping 테스트를 들 수 있다. 네트워크의 장애가 있는 경우에는 ping의 값이 안정되지 않고 높아졌다 낮아졌다 하는 변통 폭이 매우 크다. 이는 비 오는 날의 무선랜 환경에서 흔히 관찰할 수 있다.
표 2 RTT 측정 결과의 일부
21:33:39 21:33:39 3579545 937145 0.261805621
21:33:41 21:33:41 3579545 911822 0.254731258
21:33:43 21:33:44 3579545 853271 0.238374151
21:33:46 21:33:46 3579545 841814 0.235173465
21:33:48 21:33:48 3579545 848755 0.237112538
21:33:50 21:33:51 3579545 855616 0.239029262
21:33:53 21:33:53 3579545 914498 0.255478839
21:33:55 21:33:55 3579545 831402 0.232264715
21:33:57 21:33:58 3579545 877703 0.245199599
21:34:00 21:34:00 3579545 852253 0.238089757
21:34:02 21:34:02 3579545 842065 0.235243585
21:34:04 21:34:05 3579545 865826 0.241881580
21:34:07 21:34:07 3579545 869838 0.243002393
21:34:09 21:34:09 3579545 894354 0.249851308 그래프 1 RTT 측정 결과 (시간 - RTT) 그래프 2 편차가 심한 포인트를 제외한 그래프 그래프 3 RTT 산포도 (RTT - 개수)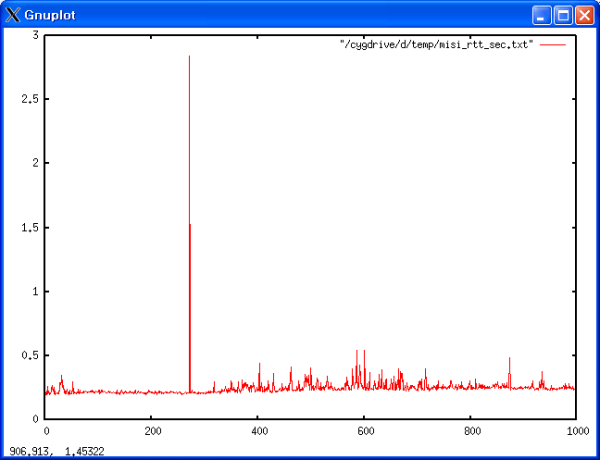
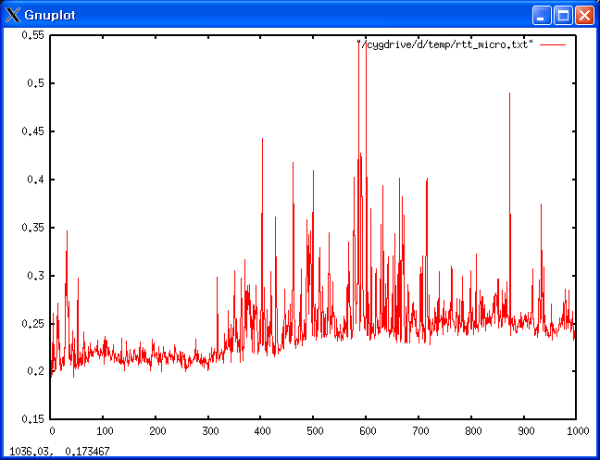
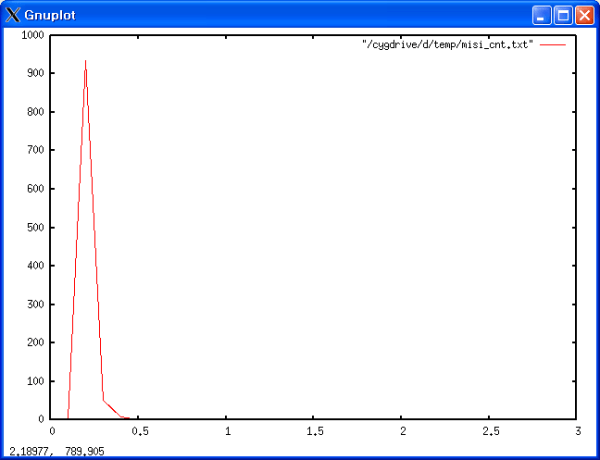
표 3 RTT 측정 결과 산포 데이터
구간 개수
0.1 ~ 0.2 3
0.2 ~ 0.3 935
0.3 ~ 0.4 51
0.4 ~ 0.5 9
0.5 ~ 0.6 2
2.8 ~ 2.9 1 거시적 관점에서의 RTT 측정 결과 분석
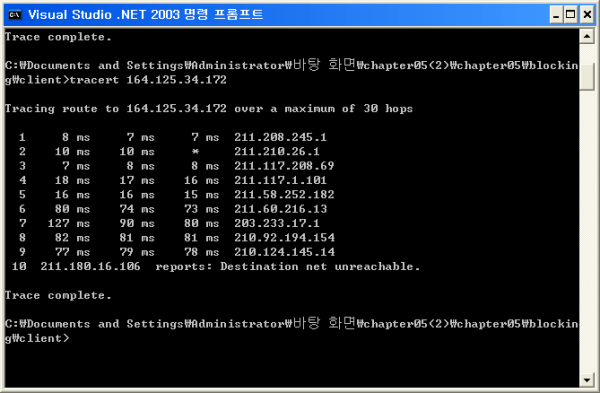
이번 실험에서는 부산시 금정구에 소재한 부산대학교 연구실과 부산시 동래구에 소재한 팀원의 집 사이의 RTT를 측정하였다. 두 지점 사이의 경로를 알아보기 위해서 tracert 유틸리티를 사용해 보았다. 하지만 실제로 두 지점 사이의 전체 경로를 구하지는 못했다. 아마도 학교측에서 막아둔 것으로 보였다. tracert의 일부 결과가 <화면 2>에 나와있다.
거시적 관점에서의 RTT를 분석하기 위해서 새벽 11시부터 오후 12시까지 30초 간격으로 총 13시간의 RTT 데이터를 수집하였다. <화면 3>에 실제 RTT를 측정하는 화면에 <표 4>에 측정 결과의 일부 데이터가 실려 있다. 화면 3 RTT 측정 화면
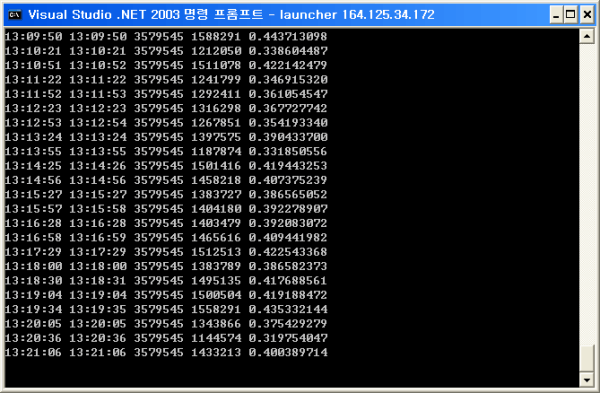
표 4 RTT 측정 결과 일부
23:20:14 23:20:14 3579545 1042587 0.291262437
23:20:44 23:20:44 3579545 1036861 0.289662792
23:21:14 23:21:15 3579545 1058471 0.295699872
23:21:45 23:21:45 3579545 1056524 0.295155949
23:22:15 23:22:16 3579545 1128048 0.315137259
23:22:46 23:22:46 3579545 1087074 0.303690553
23:23:16 23:23:17 3579545 1099739 0.307228712
23:23:47 23:23:47 3579545 1100028 0.307309449
23:24:17 23:24:17 3579545 1097900 0.306714960
23:24:48 23:24:48 3579545 1045247 0.292005548
23:25:18 23:25:18 3579545 1098739 0.306949347
23:25:48 23:25:49 3579545 1047850 0.292732736
23:26:19 23:26:19 3579545 1058111 0.295599301
23:26:49 23:26:50 3579545 1051185 0.293664418
23:27:20 23:27:20 3579545 1054592 0.294616215
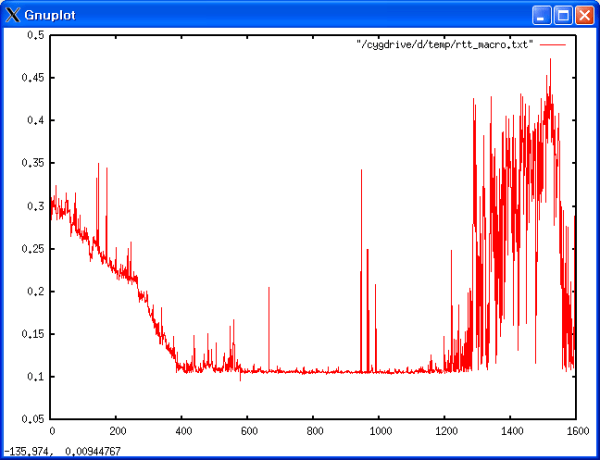
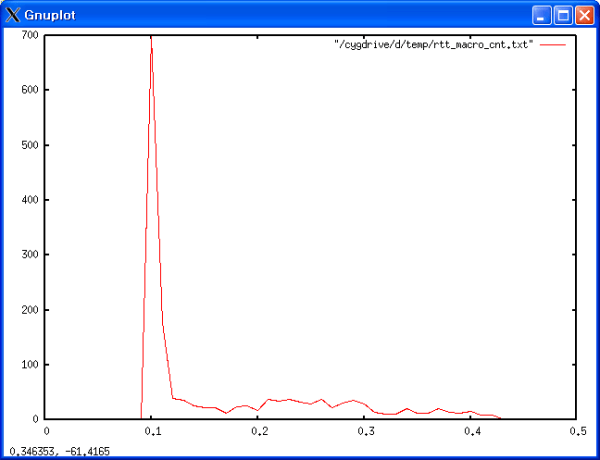
23:27:50 23:27:50 3579545 1061576 0.296567301 측정 결과를 미시적 관점과 동일하게 그래프와 산포도를 통해서 분석해 보았다. <그래프 4>, <그래프 5>, <표 6>에 결과 데이터가 나와있다. 데이터는 전체적으로 평이한 수준이었다. 그래프를 살펴보면 미시적 관점에서 분석할 때와 같은 비 정상적으로 튀는 점도 없었다. 산포도 데이터를 살펴보면 대부분의 데이터가 0.1과 0.2 사이 구간에 집중되어 있는 것을 살펴 볼 수 있다.
<그래프 4>을 한번 살펴보자. Y축의 범위가 0에서 0.5로 크지 않기 때문에 이 안에서 크게 변화한다고 해도 실제로 그렇게 큰 변화가 있었다고 보기는 힘들다. 하지만 전체적으로 구간별로 RTT가 변화하는 패턴이 다르다는 것을 볼 수 있다. 0-400사이, 400-1200사이, 1200-1600사이는 서로 다른 패턴으로 움직이고 있다. 0-400사이는 점점 RTT가 감소하고 있으며, 400에서 1200사이는 비교적 낮은 범위에서 일정한 RTT를 보여주고 있다. 1200에서 1600범위는 RTT값이 증가하였으며 미세하게 RTT값이 자주 변하는 것을 알 수 있다.
왜 그런 결과가 나왔는지 알기 위해서 우리는 데이터의 구간이 나타내는 실제 시간 범위를 살펴보았다. <표 5>에 그 결과가 나와있다. 살펴보면 실제로 우리가 인터넷을 사용하는 패턴과 일치한다고 볼 수 있다. 오후 11시부터 새벽 2시까지는 인터넷을 사용하는 사람이 계속 줄어드는 시간대다. 따라서 RTT가 지속적으로 감소 하는 결과나 나타난 것이다. 새벽 2시부터 오전 9시 까지는 인터넷을 사용하는 사람이 비교적 일정하게 유지되는 구간이다. 사람이 적고 대부분 사용하는 사람은 밤을 샐 때까지 사용할 것이다. 따라서 이 구간의 값은 비교적 낮은 값으로 일정하게 유지된 것이다. 끝으로 오전 9시부터 오후 12시 사이의 구간은 다시 인터넷을 사용하는 사람이 늘어나는 구간이다. 대부분의 회사와 학교 연구실의 출근 시간이 9시라는 점도 이러한 추측의 근거를 확실시 한다. 따라서 이 구간의 경우 RTT 값이 증가했으며 다소 불규칙하게 나온 것이다.
표 5 x축 구간별 시간 범위
구간 시간
0 - 400 PM 11:00 – AM 02:00
400 - 1200 AM 02:00 – AM 09:00
1200 - 1600 AM 09:00 – PM 12:00 이번 실험을 통해서 우리는 RTT의 변화를 통해서 인터넷의 사용 양을 측정할 수 있다는 것을 알 수 있었다. 작은 범위의 RTT 측정은 이러한 변화를 수반하기 힘들지만 장기적으로 몇 일 내지는 몇 달 동안 한 지역의 RTT를 지속적으로 측정해 보면 해당 지역의 인터넷 사용 패턴을 분석할 수 있다는 것을 알 수 있었다. 이러한 경험이 중요한 이유는 이 방법의 경우 모든 지역의 인터넷 사용을 분석하지 않고도 전체를 유추할 수 있다는 장점이다. 단지 두 대의 컴퓨터로 전체 인터넷 사용 패턴을 유추해 낼 수 있다는 것은 대단한 일이 아닐 수 없다.
표 6 RTT 측정 산포 데이터
구간 개수
0.0 – 0.1 1
0.1 – 0.2 1085
0.2 – 0.3 316
0.3 – 0.4 159
0.4 – 0.5 39