NIM 게임은 테이블 위에 놓여진 13개의 동전을 번갈아 가면서 1~3개까지 가져가서 마지막 남은 동전을 가져가는 사람이 지는 게임이다. NIM 게임에서 컴퓨터가 이기기 위한 알고리즘을 다양한 방법으로 구현해 보도록 하자.
결정 트리
13개라는 동전의 개수는 우리가 한번에 생각하기에는 너무 많은 동전의 개수다. 따라서 게임이 진행된 후 자기 차례에 4개의 동전이 남은 상황을 생각해 보자. 이 상황에서 벌어질 수 있는 모든 일이 <그림 1>에 나와있다. <그림 1>과 같은 트리를 보통 결정 트리 내지는 게임 트리라고 부른다. 이 트리는 동전이 4개 남은 상황에서 앞으로 발생할 수 있는 모든 경우를 담고 있다.
트리를 보는 방법은 간단하다. 루트에 있는 4는 현재 동전이 네 개 남아있음을 나타낸다. 자식으로 3, 2, 1이 있는 것을 볼 수 있다. 각각은 우리가 한 개, 두 개, 세 개의 동전을 가져간 경우에 테이블에 남게 될 동전의 개수다. 각각의 상황에서 상대방이 선택할 수 있는 모든 경우가 그 노드의 자식으로 있다. 예를 들면, 3개가 남은 상황에서는 상대방의 선택에 따라 테이블에 동전이 두 개, 한 개, 내지는 없을 수 있는 것이다.
자 그렇다면 4개가 남은 상황에서 우리는 이기기 위해서 몇 개의 동전을 가져가야 할까? 당연히 똑똑한 플레이어라면 3개를 집을 것이다. 왜냐하면 세 개를 가져가고 나면 테이블엔 동전이 하나 밖에 남지 않아 무조건 이기기 때문이다. 반면에 한, 두 개를 가져간 경우엔 상대방의 선택에 따라 우리가 질 수도 있다.
그림 1 테이블에 4개의 동전이 남은 경우의 결정 트리
좀 더 복잡한 상황을 생각해 보자. 5개, 6개, 7개, 8개가 테이블에 남은 상황에 대한 결정 트리가 <그림 2>에 나와있다. 5개 남은 경우엔 이길 수 있는 방법이 없고, 6개 남은 경우엔 하나를 가져감으로써 이길 수 있다. 나머지 경우에 대해서도 곰곰 생각해 보자.
그림 2 테이블에 5, 6, 7, 8개의 동전이 남은 경우의 결정 트리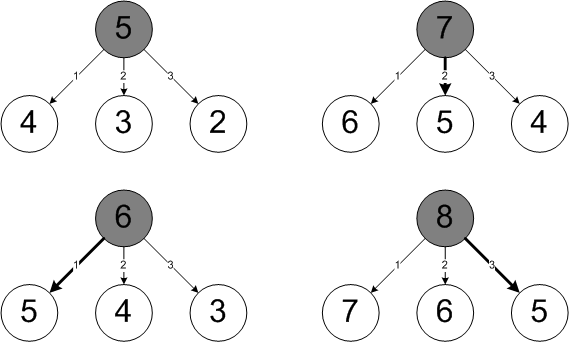
분할 정복법 (Divide-and-Conquer)
분할 정복법은 큰 문제를 여러 개의 작은 문제로 분할한 다음 각각의 결과를 결합해서 큰 문제에 대한 해답을 찾는 방법이다. 큰 문제에서 점차적으로 작은 문제로 내려가는 형태를 취하기 때문에 이런 방식의 접근 법을 하향식(top-down) 접근법이라고 부른다.
앞서 살펴본 결정 트리를 위에서 아래로 내려가면서 문제를 푼다고 생각하면 간단하다. <리스트 1>에 분할 정복법을 사용한 코드가 나와있다. IsBad는 테이블에 coins의 개수만큼 동전이 남아있는 경우에 상대방이 이길 수 있는지 없는지를 나타낸다. IsBad(1)은 당연히 TRUE가 된다. IsBad(2), IsBad(3), IsBad(5)등의 리턴 값을 앞서 게임 트리를 보면서 생각해 보도록 하자. GetCoinCount는 테이블에 n개의 동전이 남았을 때 우리가 이기기 위해서 선택해야 하는 동전의 개수를 리턴 하는 함수다. GetCoinCount(4)는 3을 리턴 한다. 만약 n개의 동전이 남은 상황에서 이길 수 있는 방법이 없다면 0을 리턴 한다. 따라서 GetCoinCount(1), GetCoinCount(5)는 0을 리턴 한다.
리스트 1 top-down 방식으로 풀어본 NIM 게임
int GetCoinCount(int coins);
int IsBad(int coins)
{
if(coins <= 1)
return TRUE;
else
return GetCoinCount(coins) == 0;
}
int GetCoinCount(int coins)
{
for(int i=1; i<=3; ++i)
{
if(coins - I <= 0)
break;
if(IsBad(coins - i))
return i;
}
return 0;
}분할 정복법은 코드를 작성하기 쉽고 직관적이라는 장점이 있다. 하지만 분할 정복법의 가장 큰 단점은 결정 트리가 커질수록 경우의 수가 많아지고 반복적인 부분이 늘어나기 때문에 코드의 수행 속도가 비 정상적으로 느려진다는 단점이 있다. 얼마나 반복적인 부분이 많이 호출 되는지 알고 싶은 독자는 GetCoinCount, IsBad 함수의 시작 부분에 각각 printf를 추가한 다음 GetCoinCount(4)를 호출해 보도록 하자.
동적 계획법 (Dynamic Programming)
동적 계획법 또한 분할 정복법과 마찬가지로 작은 문제의 답을 통해서 큰 문제의 답을 구한다는 점에서는 비슷하다. 하지만 동적 계획법은 분할 정복법과는 달리 한번 구해진 답을 계속 계산하지 않고 메모리에 저장해 두고 참고한다. 분할 정복법과 동적 계획법의 차이는 <그림 1>과 <그림 2>의 차이라고 할 수 있다. <그림 1>에는 동일한 노드가 여러 번 그려져 있다. 2개가 남은 경우에 대한 결정 트리가 두 번 포함된 것을 보면 알 수 있다. 하지만 <그림 2>에서는 이미 구해진 트리에 대한 부분은 표시를 하지 않았다. 전자가 분할 정복법 이라고 한다면, 후자의 그림은 동적 계획법이 된다. 분할 정복법이 트리를 위에서 아래로 타고 내려오는 형태라면, 동적 계획법은 트리를 하나의 노드에서 점진적으로 키워 나가는 형태를 취한다. 그래서 동적 계획법은 상향식(bottom-up) 접근 방법이다.
동적 계획법은 일반적으로 테이블을 사용해서 구현된다. 작은 문제에 대한 해답을 테이블에 기록해 둔 다음 이후에 그 값이 필요하다면 테이블을 참조해서 이미 구해진 답을 이용하는 것이다.
<리스트 2>에는 NIM 게임 테이블을 생성시키는 코드가 나와있다. GenerateNimTable 함수에 생성할 테이블 포인터와 개수를 입력하면 개수만큼 답을 구해서 테이블을 채워준다. win은 해당 노드에서 우리가 이길 수 있는지 없는지를 나타낸다. solution에는 각각의 선택에 대한 승, 패 여부가 기록된다. T가 GenerateNimTable 함수를 통해 생성한 테이블이라고 할 때, 5개가 남은 상황에서 우리가 이길 수 있는지 여부는 T[5].win을 참고하면 된다. 만약 이길 수 있는 노드라면 몇 개를 가져가야 이길 수 있는지는 T[5].solution[0], T[5].solution[1], T[5].solution[2]를 살펴보면 알 수 있다.
리스트 2 NIM 게임 테이블을 생성하는 코드
#define MAX\_SEL 3
typedef struct \_NIMITEM
{
bool win;
bool solution[MAX\_SEL+1];
} NIMITEM, \*PNIMITEM;
void GenerateNimTable(PNIMITEM tb, int last)
{
tb[1].win = false;
for(int i=1; i<=MAX\_SEL; ++i)
tb[1].solution[i] = false;
bool win;
for(int i=2; i<=last; ++i)
{
win = false;
for(int j=1; j<=3; ++j)
{
if(i-j > 0)
{
if(tb[i-j].win)
tb[i].solution[j] = false;
else
{
tb[i].solution[j] = true;
win = true;
}
}
else
tb[i].solution[j] = false;
}
tb[i].win = win;
}
}일반적으로 동적 계획법은 분할 정복법보다 이해하기 힘들고, 덜 직관적이다. 하지만 수행 속도는 분할 정복법보다 훨씬 빠르다는 장점이 있다. 왜냐하면 반복적인 부분을 다시 계산하지 않기 때문이다.
휴리스틱
휴리스틱이란 우리가 경험이나 관찰에 의해서 알고 있는 지식을 통해서 알고리즘을 설계하는 것을 말한다. 교통 신호 제어 시스템의 알고리즘을 설계할 때 출, 퇴근 시간에 붐비는 도로에 더 많은 가중치를 두는 것이 그러한 예라고 할 수 있다.
<표 1>은 앞서 살펴보았던 동적 계획법으로 만들어진 테이블의 결과를 담고 있다. 테이블을 정렬해 두어서 규칙이 쉽게 눈에 들어올 것이다. 남은 동전의 개수에서 1을 뺀 다음 4로 나눈 나머지가 이기기 위해서 우리가 선택해야 하는 동전의 개수다. 여기서 0이 나오면 그 상황에서 우리가 반드시 이길 수 있는 방법은 없다는 것을 나타낸다. <리스트 3>에는 이러한 방법을 사용해서 개수를 구하는 GetCoinCount 함수가 나와있다.
표 1 동전 개수에 대한 승, 패 여부
개수 승, 패 개수 승, 패 개수 승, 패
1 패 5 패 9 패
2 승 (1개) 6 승 (1개) 10 승 (1개)
3 승 (2개) 7 승 (2개) 11 승 (2개)
4 승 (3개) 8 승 (3개) 12 승 (3개) 리스트 3 휴리스틱 방법을 사용한 코드
int GetCoinCount(int coins)
{
return (coins - 1) % 4;
}휴리스틱 방법은 대부분의 경우 수행 속도가 빠르고, 좋은 실행 결과를 가진다는 장점이 있다. 하지만 그런 만큼 휴리스틱 알고리즘을 생각해 내기는 가장 어렵다. 물론 이렇게 간단한 문제에 대해서는 쉽게 답이 나오지만 복잡한 문제에 대해서는 몇 년을 고민해도 답이 나오지 않는 경우가 많다. 또한 휴리스틱을 사용한 코드는 별도의 주석이 없으면 나중에 유지 보수 하는 사람이 이해하기 어려운 코드가 되기 쉽다. 앞서 구현한 GetCoinCount의 경우도 왜 저렇게 하는지 부연 설명이 없다면 코드를 유지 보수하는 사람에게는 마치 마법 같은 코드가 되는 것이다. 따라서 이러한 코드에는 반드시 숫자들이 어디서 왔는지 그리고 그 원리가 무엇인지를 주석으로 남겨둘 필요가 있다.